Differentially personal heatmaps– Google AI Blog Site

Just recently, differential personal privacy (DP) has actually become a mathematically robust concept of user personal privacy for information aggregation and artificial intelligence (ML), with useful implementations consisting of the 2022 United States Census and in market. Over the last couple of years, we have open-sourced libraries for privacy-preserving analytics and ML and have actually been continuously improving their abilities. On the other hand, brand-new algorithms have actually been established by the research study neighborhood for numerous analytic jobs including personal aggregation of information.

One such crucial information aggregation approach is the heatmap Heatmaps are popular for envisioning aggregated information in 2 or more measurements. They are extensively utilized in numerous fields consisting of computer system vision, image processing, spatial information analysis, bioinformatics, and more. Securing the personal privacy of user information is vital for numerous applications of heatmaps. For instance, heatmaps for gene microdata are based upon personal information from people. Likewise, a heatmap of popular areas in a geographical location are based upon user place check-ins that require to be kept personal.

Inspired by such applications, in “ Differentially Personal Heatmaps” (provided at AAAI 2023), we explain an effective DP algorithm for calculating heatmaps with provable assurances and examine it empirically. At the core of our DP algorithm for heatmaps is a service to the standard issue of how to independently aggregate sporadic input vectors (i.e., input vectors with a little number of non-zero collaborates) with a little mistake as determined by the Earth Mover’s Range (EMD). Utilizing a hierarchical segmenting treatment, our algorithm views each input vector, in addition to the output heatmap, as a possibility circulation over a variety of products equivalent to the measurement of the information. For the issue of sporadic aggregation under EMD, we provide an effective algorithm with mistake asymptotically near to the very best possible.

Algorithm description

Our algorithm works by privatizing the aggregated circulation (acquired by balancing over all user inputs), which suffices for calculating a last heatmap that is personal due to the post-processing residential or commercial property of DP This residential or commercial property makes sure that any improvement of the output of a DP algorithm stays differentially personal. Our primary contribution is a brand-new privatization algorithm for the aggregated circulation, which we will explain next.

The EMD procedure, which is a distance-like procedure of significant difference in between 2 likelihood circulations initially proposed for computer system vision jobs, is appropriate for heatmaps considering that it takes the underlying metric area into account and thinks about “surrounding” bins. EMD is utilized in a range of applications consisting of deep knowing, spatial analysis, human movement, image retrieval, face acknowledgment, visual tracking, shape matching, and more.

To attain DP, we require to include sound to the aggregated circulation. We would likewise like to maintain data at various scales of the grid to reduce the EMD mistake. So, we produce a hierarchical partitioning of the grid, include sound at each level, and after that recombine into the last DP aggregated circulation. In specific, the algorithm has the following actions:.

1. Quadtree building and construction: Our hierarchical segmenting treatment very first divides the grid into 4 cells, then divides each cell into 4 subcells; it recursively continues this procedure up until each cell is a single pixel. This treatment develops a quadtree over the subcells where the root represents the whole grid and each leaf represents a pixel. The algorithm then determines the overall likelihood mass for each tree node (acquired by accumulating the aggregated circulation’s possibilities of all leaves in the subtree rooted at this node). This action is shown listed below.
   

   In the initial step, we take the (non-private) aggregated circulation ( leading left) and consistently divide it to produce a quadtree. Then, we calculate the overall likelihood mass is each cell ( bottom).

2. Sound addition: To each tree node’s mass we then include Laplace sound adjusted to the usage case.
3. Truncation: To help in reducing the last quantity of sound in our DP aggregated circulation, the algorithm passes through the tree beginning with the root and, at each level, it disposes of all however the top w nodes with greatest (loud) masses together with their descendants.
4. Restoration: Lastly, the algorithm fixes a direct program to recuperate the aggregated circulation. This direct program is motivated by the sporadic healing literature where the loud masses are deemed (loud) measurements of the information.

In action 2, sound is contributed to each cell’s likelihood mass. Then in action 3, just top-w cells are kept ( green) whereas the staying cells are truncated ( red). Lastly, in the last action, we compose a direct program on these leading cells to rebuild the aggregation circulation, which is now differentially personal.

Speculative outcomes

We examine the efficiency of our algorithm in 2 various domains: real-world place check-in information and image saliency information. We think about as a standard the common Laplace system, where we include Laplace sound to each cell, absolutely no out any unfavorable cells, and produce the heatmap from this loud aggregate. We likewise think about a “thresholding” variation of this standard that is more matched to sporadic information: just keep leading t% of the cell worths (based upon the likelihood mass in each cell) after noising while zeroing out the rest. To examine the quality of an output heatmap compared to the real heatmap, we utilize Pearson coefficient, KL-divergence, and EMD. Keep in mind that when the heatmaps are more comparable, the very first metric boosts however the latter 2 decline.

The areas dataset is acquired by integrating 2 datasets, Gowalla and Brightkite, both of which consist of check-ins by users of location-based socials media. We pre-processed this dataset to think about just check-ins in the continental United States leading to a last dataset including ~ 500,000 check-ins by ~ 20,000 users. Thinking about the leading cells (from a preliminary partitioning of the whole area into a 300 x 300 grid) that have check-ins from a minimum of 200 distinct users, we partition each such cell into subgrids with a resolution of ∆ × ∆ and designate each check-in to among these subgrids.

In the very first set of experiments, we repair ∆ = 256. We evaluate the efficiency of our algorithm for various worths of ε (the personal privacy specification, where smaller sized ε suggests more powerful DP assurances), varying from 0.1 to 10, by running our algorithms together with the standard and its versions on all cells, arbitrarily tasting a set of 200 users in each trial, and after that calculating the range metrics in between the real heatmap and the DP heatmap. The average of these metrics exists listed below. Our algorithm (the red line) carries out much better than all variations of the standard throughout all metrics, with enhancements that are particularly considerable when ε is not too big or little (i.e., 0.2 ≤ ε ≤ 5).

Metrics balanced over 60 runs when differing ε for the place dataset. Shaded locations suggest 95% self-confidence period.

Next, we study the result of differing the number n of users. By repairing a single cell (with > > 500 users) and ε, we differ n from 50 to 500 users. As forecasted by theory, our algorithms and the standard carry out much better as n increases. Nevertheless, the habits of the thresholding versions of the standard are less foreseeable.

We likewise run another experiment where we repair a single cell and ε, and differ the resolution ∆ from 64 to 256. In contract with theory, our algorithm’s efficiency stays almost consistent for the whole variety of ∆. Nevertheless, the standard suffers throughout all metrics as ∆ boosts while the thresholding versions periodically enhance as ∆ boosts.

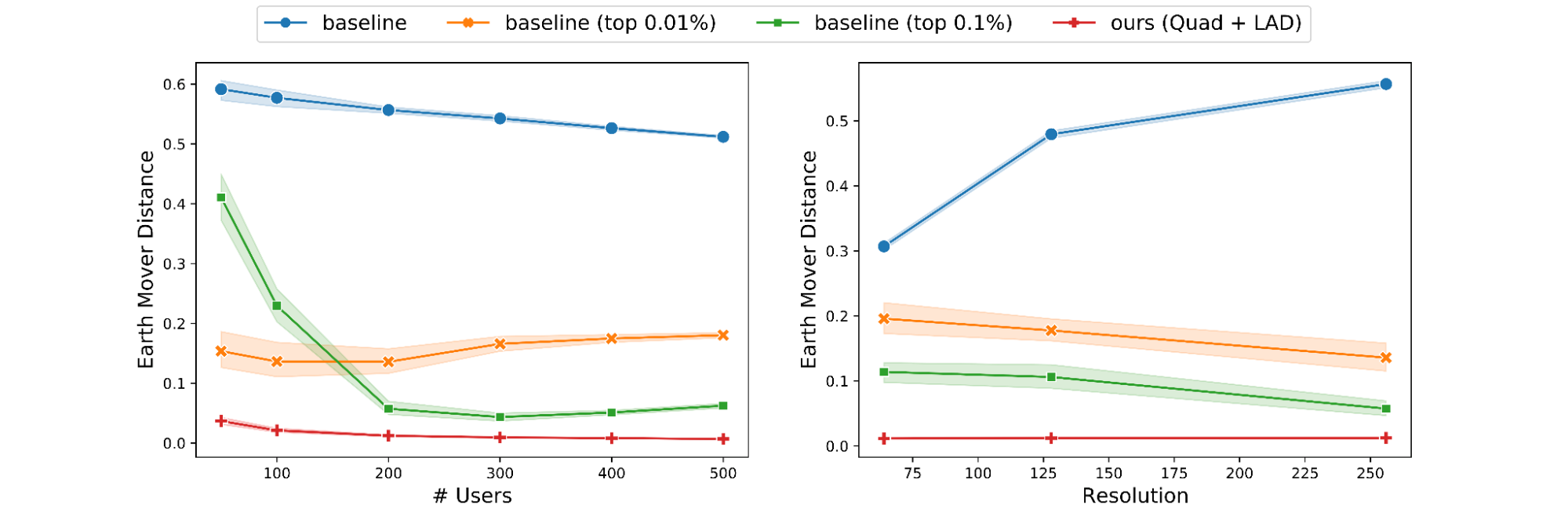Impact of the variety of users and grid resolution on EMD.

We likewise experiment on the Salicon image saliency dataset (SALICON). This dataset is a collection of saliency annotations on the Microsoft Typical Things in Context image database. We scaled down the images to a set resolution of 320 × 240 and each [user, image] set includes a series of collaborates in the image where the user looked. We duplicate the experiments explained formerly on 38 arbitrarily tested images (with ≥ 50 users each) from SALICON. As we can see from the examples listed below, the heatmap acquired by our algorithm is extremely close to the ground fact.

Example visualization of various algorithms for 2 various natural images from SALICON for ε = 10 and n = 50 users. The algorithms from delegated right are: initial heatmap (no personal privacy), standard, and ours.

Extra speculative outcomes, consisting of those on other datasets, metrics, personal privacy specifications and DP designs, can be discovered in the paper.

Conclusion

We provided a privatization algorithm for sporadic circulation aggregation under the EMD metric, which in turn yields an algorithm for producing privacy-preserving heatmaps. Our algorithm extends naturally to dispersed designs that can carry out the Laplace system, consisting of the safe aggregation design and the shuffle design This does not use to the more strict regional DP design, and it stays a fascinating open concern to develop useful regional DP heatmap/EMD aggregation algorithms for “moderate” variety of users and personal privacy specifications.

Recommendations

This work was done collectively with Junfeng He, Kai Kohlhoff, Ravi Kumar, Pasin Manurangsi, and Vidhya Navalpakkam.